Morning! Over the past few days, I have been working on relative frequency and theoretical probability. As the main task in this, I carried out a two-day investigation to discover the experimental probability of rolling at least one six with three dice and comparing it to the theoretical probability.
What are relative frequency, and experimental and theoretical probabilities?
Relative frequency is how many times a certain event happens in a certain number of tests. In this case, it was how many times I got at least one six with three dice in ten rolls (I counted all three die as one roll). To calculate the relative frequency, I divided the number of times the event happened by the amount of rolls. For example, the event happened four times in the first ten rolls, giving a relative frequency of 0.4. Relative frequencies can be used to find the experimental probability (the chance of something happening based on testing). Meanwhile, theoretical probability is the theoretical chance of something happening. For example, the theoretical probability of rolling a six with a six-sided dice is 1/6 as there are six options and rolling a six is only one of them. If the experimental and theoretical probabilities are roughly equal, then the die, spinner, etc. is probably fair.
How did we find the theoretical probability?
Finding the theoretical probability took two main stages. The first was easy: finding the total number of outcomes. Knowing that each dice could only give a total of six different outcomes, we cubed six (multiplied it by itself twice). This gave a total of 216 possible outcomes.
The second step (finding how many outcomes would give at least one six) was trickier. To begin with, we made a list of all possible outcomes with two dice and counted each one that gave at one or two sixes. However, (as we later realised) we had counted the outcome of two sixes as two separate outcomes. Next, we factored in the third die. Unfortunately, the total of qualifying outcomes (48) seemed wrong and wasn’t close to the 91 that ChatGPT was saying. We went back and found a previous mistake but this only decreased the number of outcomes. Just as our brains were about to explode, I had a breakthrough: I realised that when the second die was a six, every outcome with it would qualify. This gave us eleven outcomes that qualified when the first dice landed on a one, two, three, four or five for a total of 55. This also led to the realisation that all 36 outcomes when the first die landed on a six counted, giving us a grand (and correct) total of 91 outcomes. Finally, we converted the theoretical probability of 91/216 into a decimal (0.42).
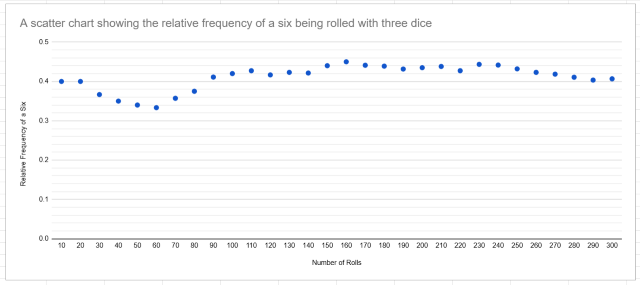
What were the results and what do they show?
The original 50 rolls showed the relative frequency tending towards 0.35, suggesting that at least one die was unfair. However, we ended up doing an extra 250 rolls, wondering what a larger sample of results would show. With a total of 300 rolls and 122 cumulative results with at least one six, the relative frequency is now tending towards 0.42, suggesting that all three dice are fair.